El món de les matemàtiques.....

• El nombre Pi (π)

• Del 3,1415..........., fins a l’infinit

• Des de l'antiguitat fins als superordinadors actuals

• Aplicacions en la geometria, trigonometria i física

• Diverses ciències actuals i part del nostre futur

• 3/14 - Data del naixement d'Albert Einstein en 1879

Fa un parell de dies publicàvem l’article de referència per al Dia Internacional de les Matemàtiques, i que avui volem completar respecte a una gran incògnita, “el nombre Pi (π)”. Aquesta constant matemàtica “Pi (π)” que ha sigut molt significativa a través de la història, que ens acompanya en l’actualitat e indispensable per veure el futur.

Motiu pel qual des del 2009, la Cambra de Representants dels Estats Units va aprovar la creació de la Diada o Dia Internacional, la data escollida va ser la més representativa 3/14, que són les xifres inicials del nombre PI (π), és a dir 3,1415............ fins a l’infinit.

La celebració del nombre PI, és també la data que es commemora el naixement d'Albert Einstein en 1879.

Però.... Què és el nombre PI?

S'entén com a nombre PI, al nombre que s'obté en dividir la longitud d'una circumferència pel seu diàmetre. És considerat un nombre irracional, així com una constant matemàtica de gran valor.

El nombre PI, és la relació entre la longitud d'una circumferència i el seu diàmetre.

És molt usat per a resoldre problemes matemàtics, de la física i també en el món de l'Enginyeria.

La Història del nombre

Pel que sembla, el nombre “PI” és molt antic. Es creu que ha sigut utilitzat des de fa milers d'anys, molt abans dels babilonis. Per als egipcis, el nombre pi tenia molt a veure amb la construcció de les piràmides i també els xinesos tenen moltes històries per a contar d'aquest extraordinari i misteriós nombre.

Grans científics i matemàtics com Isaac Newton van aconseguir desxifrar alguns dels seus dígits Amb el transcórrer dels anys, altres genis de les matemàtiques i la física, van poder calcular un nombre més gran de dígits.

Fins a la present data, resulta impossible calcular l'àrea exacta de la circumferència, ja que Pi és un nombre infinit.

Ramon Llull deia....

L'Any 1299, Ramon Llull, al seu llibre "De quadratura e triangulatura de cercle", afirmà que amb el compàs no es pot mesurar la circumferència.

Deixà escrit en català antic.... “Com siasso que mesures de linyes dretes e mesures de linyes circulars no sien de una mateixa raho e ab lo compas hom no pusca mesurar linyes circulars ab linyes dretes, per aço coue en l'anjma mesurar linyes dretes e circulars ab la ymaginacio matematicalmen rehebent los significats de linyes dretes e circulars sentides en sobiet visible”

Aquesta conjectura és equivalent a afirmar que és irracional i, a més a més, és un nombre no construïble.

L’Era informàtica

A principis del segle XX, el matemàtic indi Srinivasa Ramanujan va trobar moltes fórmules per calcular π; algunes destaquen per la seva elegància i profunditat matemàtica.

Una de les seves fórmules és la sèrie,

També cal destacar la sèrie relacionada formulada pels germans Chudnovsky el 1987.

Sèrie que genera 14 xifres per a cada terme. A finals dels 1980, els Chudnovsky van fer servir aquesta fórmula per establir uns quants rècords de càlcul de π, entre ells, el primer càlcul de més de mil milions de xifres decimals, exactament 1.011.196.691 xifres, que establiren el 1989. Continua sent la fórmula que es fa servir en els programaris per a calcular π en els ordinadors personals, però no la dels superordinadors que s'usen per establir els rècords més actuals.

“Un algorisme o algoritme és un conjunt finit d'instruccions
o passos que serveixen per a executar una tasca o resoldre un problema”

Mentre que les sèries normalment augmenten la precisió amb una quantitat fixa per a cada terme afegit, hi ha algorismes iteratius que a cada pas “multipliquen” el nombre de xifres correctes. L'any 1975 es va realitzar un progrés significatiu quan Richard Brent i Eugene Salamin, de manera independent l'un de l'altre, van descobrir l'algorisme de Brent-Salamin, que només fa servir aritmètica per doblar el nombre de xifres correctes a cada pas.

L'algorisme consisteix a establir.....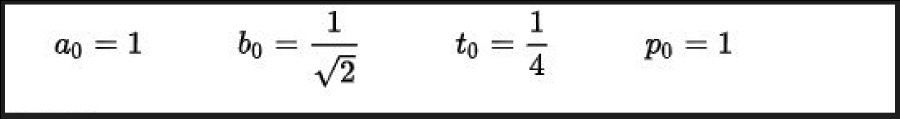
i iterar....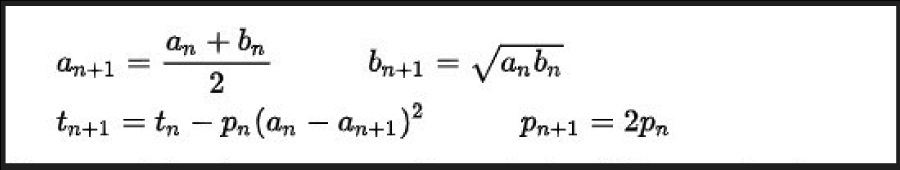

fins que an i bn estan prou a prop. Llavors l'estimació de π ve donada per.....

Fent servir aquest sistema, amb 25 iteracions n'hi ha prou per obtenir 45 milions de decimals correctes. Jonathan i Peter Borwein van trobar un algorisme similar que quadruplica l'exactitud a cada pas.

Més recentment, una important contribució va ser la fórmula de Bailey–Borwein–Plouffe (fórmula BBP), descoberta per Simon Plouffe, anomenada així en honor dels autors de l'article on per primer cop es va publicar la fórmula: Bailey, Borwein i Plouffe.
La fórmula.....

És singular perquè permet trobar qualsevol dígit individual hexadecimal o binari de π sense haver de calcular tots els precedents.

Entre el 1998 i el 2000, el projecte de computació distribuïda PiHex va fer servir una modificació de la fórmula BBP deguda a Fabrice Bellard (fórmula de Bellard) per calcular el bit de π en posició mil bilions (1015), que va resultar ser 0. El setembre de 2010, un empleat de Yahoo! utilitzà l'aplicació Hadoop en mil ordinadors durant un període de 23 dies per calcular 256 bits de π al bit en posició dos mil bilions (2×1015).

La xifra més gran fins a la data és de 5 bilions de decimals, assolida el 2010 per l'estudiant nord-americà Alexander Yi i l'investigador japonès Shigeru Kondo.

Més dades curioses

Aquest enigmàtic nombre presenta algunes dades curioses, entre les que recollim algunes:

• Per als científics ha estat un repte esbrinar els misteris que tanca el nombre pi. L'any 2014 amb l'ús d'un ordinador modern, van poder descobrir que tanca més de 12,1 bilions de dígits i que sembla no tenir fi.
• El nombre PI, és emprat per a la fabricació de rellotges i per a l'estudi de l'Astronomia.
• Amb aquest nombre, s'han trencat alguns rècords, com el del japonès Akira Araguhci, qui en el 2006, va recitar 100.000 dígits del nombre pi, emprant en això 16 hores seguides, només parant per a beure aigua.
• El matemàtic Ludolph Van Ceulen va ordenar que posessin en la seva làpida els 35 dígits del nombre pi que havien estat calculats per aquest.